The product of two sets can be written as \( A \times B = \{(x, y)\ |\ x \in A, y \in B \} \). This is a perfectly good way to think about products, but there is another way: their universal property.

The product of sets \( A \) and \( B \) is a set \( X \) along with functions \( \pi_1 : X \to A \), \( \pi_2 : X \to B \) such that for any set \( T \) with functions \( f : T \to A \), \( g : T \to B \), there is a unique function \( h : T \to X \) such that \( f = \pi_1 \circ h \) and \( g = \pi_2 \circ h \).

We can verify that our original definition of products satisfies this property. The functions in question will be \( \pi_1((x,y)) = x \) and \( \pi_2((x,y)) = y \). Then if we have functions \( f : T \to A \), and \( g : T \to B \), the unique function \( h : T \to A \times B \) is \( h(t) = (f(t), g(t)) \).

However, the universal property as I wrote it above is difficult to remember. Here's a better way to say it:

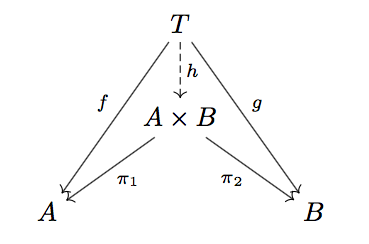
This is a commutative diagram, which means that for any two paths with the same start point and end point, the compositions of functions along those two paths are equal. In this diagram, that is the conditions \( f = \pi_1 \circ h \) and \( g = \pi_2 \circ h \).

This diagram can be thought of as the shape of a product. With this shape in mind, and only this shape, we can prove some important properties.

If two sets \( X \) and \( X' \) both satisfy the universal property for the product of \( A \) and \( B \), then they are isomorphic.

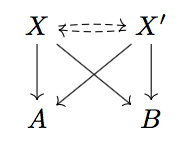
By applying the universal property for \( X \) with \( X' \) as \( T \), we get a function \( X' \to X \) that commutes with the projection maps. Similarly, applying the universal property for \( X' \) with \( X \) as \( T \), we get a function \( X \to X' \) that commutes with the projection maps. Composing these two functions, we get functions \(X \to X\) and \(X' \to X'\) that commute with the projection maps.

However, by applying the universal property for \( X \) with itself as \( T \), we see that there is only one function \( X \to X \) that commutes with the projection maps, and the identity function is such a function, so it must be the only one. This means that the composition \(X \to X\) from before must be the identity, and similarly the composition \(X' \to X'\) must be the identity, so the two functions define an isomorphism.

This justifies our use of the universal property as a complete description of a product, and in fact shows us that any product will be isomorphic to the explicit definition that we had at the beginning of this post.

For any three sets \( A \), \( B \), \( C \), we have \( (A \times B) \times C \) and \( A \times (B \times C) \) are isomorphic.

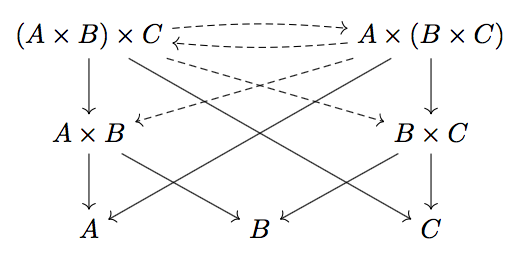
First we draw the basic shapes for \( A \times B \), \( B \times C \), \( (A \times B) \times C \), and \( A \times (B \times C) \). Then notice that the diagram contains maps \( (A \times B) \times C \to B \) (through the path \( (A \times B) \times C \to A \times B \to B \)) and \( (A \times B) \times C \to C \), so we get a unique map \( (A \times B) \times C \to B \times C \) commuting with the diagram.

Then we have maps \( (A \times B) \times C \to A \) and \( (A \times B) \times C \to B \times C \), so we get a unique map \( (A \times B) \times C \to A \times (B \times C) \) commuting with the diagram. Similarly, we get a unique map in the other direction, and by a similar argument to before, the compositions in both directions must be the identity.

Most algebraic concepts, and many lemmas, have a shape in the same way that products do. Often, these are universal properties, but sometimes they are less restrictive. In many cases, the shapes are much simpler than the corresponding explicit constructions, so when presented with an algebraic statement, drawing out the diagram makes appropriate lemma applications much more clear. Sounds a lot like how people describe solving geometry problems.